Ik zie dat mijn link niet goed doorkomt. Hier het verhaal:
1 Motorkoppel
Het motorkoppel kan worden beschouwd als de ’kracht waarmee de motor
ronddraait’. De kracht F op de zuigerpen, veroorzaakt door de verbrandingsdruk
p, wordt uiteindelijk uitgeoefend op de krukstraal r waardoor een koppel
M = Ft x r ontstaat (fig. 1). Voor de begripsbepaling kunnen we onthouden dat
de (verbrandings)kracht op de zuiger vermenigvuldigt met de krukstraal een
koppel veroorzaakt dat bekend staat onder het motorkoppel. In werkelijkheid
ligt het allemaal ingewikkelder omdat de druk op de zuiger gedurende het
vierslagproces sterk vari¨eert en dat de hoek van de krachtoverbrenging op de
kruktap steeds verandert. We dienen dan met gemiddelde waarden te werken.
De verbrandingsdruk p op de zuiger is een gemiddelde waarde en wordt uit het
indicateurdiagram of pv-diagram gehaald (fig. 2). We kunnen dit doen door
grafisch de gemiddelde hoogte te bepalen tussen de compressie- en arbeidslijn.
Door de wisselende verbrandingsdruk en het kruk-drijfstangmechanisme zal
ook de tangentiaalkracht geen constante grootheid zijn. We werken dan ook
met de gemiddelde tangentiaalkracht. Deze kan grafisch met behulp van fig.
3 worden bepaald. Het motorkoppel hangt uitsluitend af van de kracht op de
zuiger omdat de andere grootheden zoals de zuigerdiameter en de krukstraal
vaste motorgegevens zijn. De kracht op de zuiger wordt veroorzaakt door de
verbrandingsdruk en deze hangt weer af van de vullingsgraad van de motor
(bij sto¨ıchiometrische mengverhouding). Het is in hoofdzaak de smoring in
het inlaatspruitstuk die de vullingsgraad van de motor bepaalt. De grootste
smoring wordt veroorzaakt door de stand van de gasklep zodat we kunnen
stellen dat de gasklepstand de grootste invloed heeft op het motorkoppel.
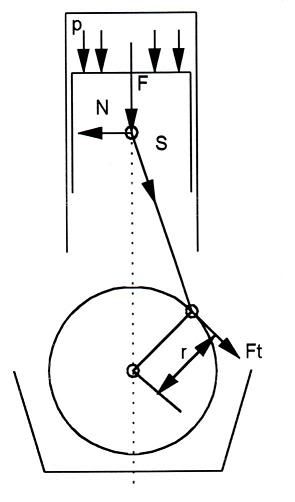Figuur 1: De verbrandingsdruk p op de zuiger geeft via de zuigerpen een kracht op de drijfstang.
De kracht op de drijfstang geeft op zijn beurt een kracht op de kruktap, de zgn. tangentiaalkracht
(Ft). Het koppel Ft x r wat daar een gevolg van is wordt uitgedrukt in Nm.
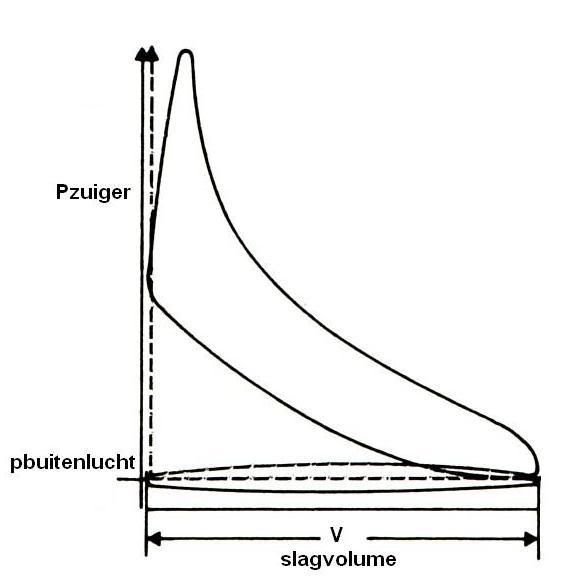Figuur 2: Het indicateurdiagram van een vierslagmotor. Uit dit diagram kan de gemiddelde druk
op de zuiger worden bepaald.
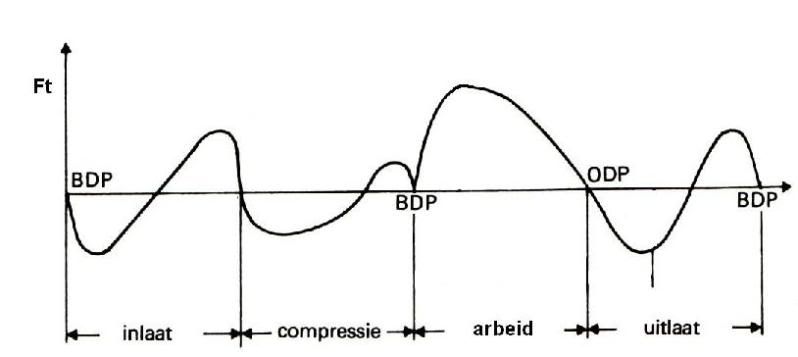Figuur 3: De tangentiaal kracht is in werkelijkheid een kracht die voortdurend van grootte en
richting verandert. We werken dan ook met de gemiddelde tangentiaalkracht Ft.
En dat is ook zo. We be¨ınvloeden immers de motorprestatie door de gasklepstand
te veranderen. Wanneer we echter het motorkoppel op een proefstand willen
meten dan zijn we in de meeste gevallen ge¨ınteresseerd in het maximum
motorkoppel. De meeste testen worden dan ook uitgevoerd met de gasklep
volledig open. Voor het verkrijgen van een motorkoppel is theoretisch geen
toerental nodig. Immers een verbranding op de zuiger bij geblokkeerde motor
geeft wel degelijk een motorkoppel. Dat het koppel bij een verbrandingsmotor
niet denkbaar is zonder motortoerental wordt veroorzaakt door het feit dat
voor het aanzuigen, comprimeren etc. krukasrotatie nodig is.
Wanneer we onze redenering volgen dan zal -bij volledig geopende gasklepbij
alle toerentallen het motorkoppel gelijk blijven. In theorie is dit ook zo.
Alleen zal ten gevolge van de veranderende gassnelheden en de vaste klepopeningshoeken
de vullingsgraad -ondanks het feit dat de gasklep geheel geopend
is- niet gelijk blijven. Slechts in ´e´en klein toerengebied zal de vullingsgraad
optimaal zijn. Hiervoor en hierna zal het motorkoppel lager zijn. Fig. 4 geeft
het koppel aan bij verschillende toerentallen bij geheel geopende gasklep.
We zien dat -in dit voorbeeld -bij zo’n 2000 t/min. (ongeveer 30 Hz) het
motorkoppel het grootst is. Dit is dan ook het toerental waarbij de het voertuig
zijn grootste trekkracht ontwikkeld. Wanneer we het motorkoppel zouden gaan
meten bij verschillende standen van het gaspedaal dan zouden we het verloop
als fig. 5 kunnen voorstellen. Deze metingen worden echter zelden uitgevoerd.
Het koppel is direct verantwoordelijk voor de trekkracht van de auto. Het
motorkoppel wordt dan vermenigvuldigd met de overbrengverhouding i van
versnellingsbak en eindreductie en gedeeld door de belaste straal (rb) van de
aangedreven wielen. Voorbeeld:
max. motorkoppel 100 Nm bij 3000 t/min.
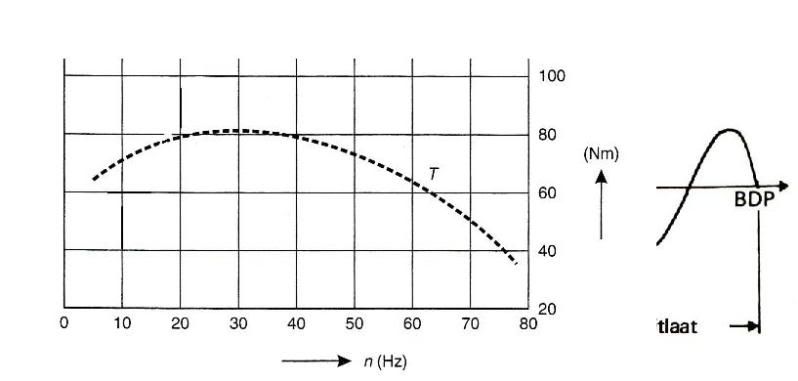Figuur 4: Het motorkoppel gemeten bij volledig ingetrapt gaspedaal bij verschillende motortoerentallen.
Het betreft hier een geıdealiseerde grafiek.
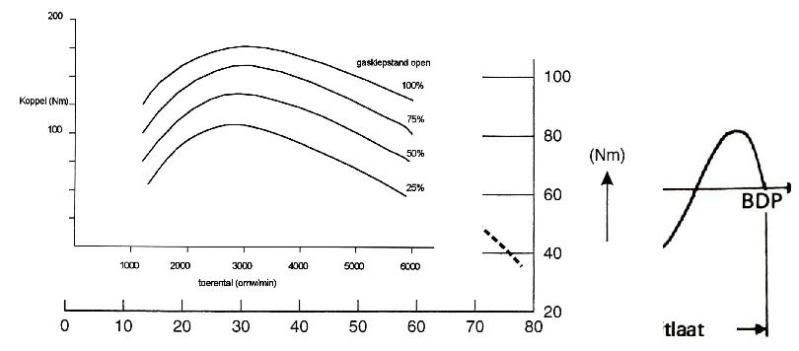Figuur 5: Het koppelverloop bij diverse toerentallen bij verschillende standen van de gasklep.
1e versnelling: i = 4
eindreductie: i = 3
rb= 0,3 m
Gevraagd:
a) trekkracht aan de aangedreven wielen
b) rijsnelheid van de auto
Oplossing:
a) F trekkracht = (100 Nm x 4 x 3) / 0,3 m = 4000 N
b) Toerental wielen = 3000 t/min / (3 x 4) = 250 t/min = 4,17 omw/s
1 omw. wiel = 2 x x 0,3 m = 1,88 m
voertuigsnelheid = 4,17 omw/s x 1,88 m = 7,84 m/s = 28,2 km/h
Het motorkoppel van een motor wordt gemeten door de motor bij verschillende
toerentallen af te remmen. Dit houdt in dat we de motor bij
volledig geopende gasklep laten draaien op bijv. 1500, 2000, 2500, 3000 etc.
tot 6000 t/min. Door de motor af te remmen wordt het gekozen toerental
constant gehouden. De afremkracht van de motor vermenigvuldigt met de
arm waarop de kracht werkt is dan het motorkoppel. Het afremmen van de
motor geschiedt op een proefstand waarvan het afremmen op verschillende
manieren kan gebeuren. Vaak wordt gebruik gemaakt van een lucht- of watergekoelde
wervelstroomrem (elektromagneten wekken in een metalen schijf
wervelstromen op) waarbij de afremkracht bepaald wordt door de verbuiging
van torsie-element te meten. Fig. 6 geeft de opstelling van een motor op
een proefstand weer. Koppel en vermogen worden via de Personal Computer
weergegeven.
In de tabel van fig. 7 zijn 12 verschillende automotoren met vier kleppen per
cilinder opgenomen die met elkaar te vergelijkbaar zijn maar verschillende
eigenschappen vertonen. Let bijv. op het toerenverschil waarbij het maximum
koppel optreedt bij de Mitsubishi en de Rover.
Mitsubishi: 175 Nm bij 5500 t/min.
Rover: 184 Nm bij 2500 t/min.
We mogen- weliswaar met enige voorzichtigheid- stellen dat een ’toer’wagen
het maximale koppel legt bij een relatief laag toerental en een ’sport’wagen het
maximale koppel op een hoger toerental. Dit verschil in motorkarakter werd
tot voor kort voornamelijk verkregen door de kleptiming (het openen en sluiten
van de kleppen) te wijzigen. Tegenwoordig spelen meer zaken als variabele
kleptiming, drukvulling en variabele spruitstuklengte een rol.
Het maximale koppel zegt niet alles. Een snelle stijging van het koppel tussen
2000 en 5000 t/min is bijv. beter dan een hoge maximale waarde. Alleen
een koppelkromme laat deze verschillen zien. Een vlakker verloop van de kop-
pelkromme wordt verkregen door variabele kleptijden en variabele lengte /
doorsnede van het inlaatspruitstuk. Deze gegevens kunnen we echter niet uit
de tabel halen. Hetzelfde geldt voor het maximale vermogen. Om vermogen en
koppel te kunnen beoordelen hebben we meer nodig dan alleen een paar getallen.
Deze informatie wordt gegeven door middel van een koppel- en vermogensgrafiek.
Bij de oudere tweeklep-motoren neemt het motorkoppel langzaam
toe. Bij moderne motoren neemt het motorkoppel snel toe, vlakt dan af maar
neemt door de inlaatspruitstukregelingen nog steeds toe tot zo’n 5000 t/min.
Het koppelverloop be¨ınvloedt niet alleen het rijgedrag van de auto maar ook
het verbruik en de uitlaatgasemissie. De technische ontwikkelingen bewegen
zich in de richting van:
meerkleppen motoren;
variabele kleptiming;
variabele inlaatspruitstuklengte / doorsnede;
in- en uitschakelbare cilinders;
turbo(compressor)motoren;
2 Motorvermogen
Veel bekender dan het motorkoppel is het motorvermogen. Motorvermogen is
het motorkoppel vermenigvuldigt met het motortoerental. Het vermogen is eigenlijk
hoeveel maal het koppel per seconde kan worden geleverd. De eenheid
is dan ook de Nm/s of Watt. De offici¨ele formule luidt:
P = M x ! (Voor M wordt ook wel T gebruikt)
waarin P het vermogen is in Nm/s of Watt
waarin M (T) het koppel is in Nm
en ! (omega) de hoeksnelheid is.
Nu is de hoeksnelheid (!) gelijk aan: 2 x x n waarin n gelijk is aan
het aantal omw/s.
De vermogensformule gaat dan over in:
P = M x 2 x n
Voorbeeld.
Gegeven: Koppel motor 80 Nm
Toerental waarbij dit koppel wordt bereikt: 30 omw/sec. (1800 t/min.)
Gevraagd: Het motorvermogen bij het gegeven toerental.
Oplossing: Het geleverde vermogen bij 1800 t/min. bedraagt:
P = 80 Nm x 2 x 3,14 x 30 Hz = 15072 Watt of 15 kW.
Het vermogensverloop wordt weergegeven door middel van een vermogenskromme.
Aangezien het vermogen een afgeleide is van het koppel is het
logisch dat beide grafieken samen worden weergegeven.
.